꿈돌이의 얄팍다식: 유클리드 기하학(밧줄로 정다각형, 타원, 포물선, 쌍곡선 작도), 원주율, 황금비, 복사지/복사용지 종횡비

2024-06-28-금 수정

유클리드 기하학(밧줄로 정다각형 작도), 원주율, 황금비, 복사지/복사용지 종횡비

옛날에 건축이나 농지 면적 계산을 할 때 밧줄이나 실을 이용해서 측정을 했다. 밧줄로 원과 직선을 그릴 수 있었다. 자와 컴퍼스는 필요 없다. 이런 작은 것으론 땅 위에 큰 원과 긴 직선을 못 그린다. 여하튼 그 과정에서 기하학이 탄생하고 유클리드가 그런 방법들을 모아 깔끔하게 증명하여 정리했다. 고대 이름 없는 천재들이 발견한 것들을 모두 모아 놓으면 그게 학문이다. 그런 이유로 증명이 없었지만 정답인 것을 이미 알고 있는 방법들도 있었다. 원리는 모르겠으나 실험적으로 증명된 방법들 말이다.

가장 간단한 동양의 피타고라스 정리 증명

※ 페르마의 정리 : 직각 삼각형 3변에 대해 aⁿ + bⁿ = cⁿ, n > 2, abc ≠ 0 조건을 만족하는 (a, b, c) 세 쌍의 수는 없다. 당연하겠지. 직각 삼각형의 (a, b, c) 세 쌍의 수는 당연히 a² + b² = c² 조건을 만족 시키니까 좌우에 같은 숫자 x만 곱해야 등식이 성립하지. 3승 이상에 대해 조건을 만족하려면 x = a = b= c 가 되어야 하는데, 이런 x는 0 외엔 없지. 또한 a = b = c의 경우는 정삼각형이라 피타고라스 정리를 만족 시킬 수 없지.

아래는 기초적인 작도 방법이다. 자가 없어도 정확하게 길이와 각도를 측정할 수 있는 방법이다. 자와 각도계를 만들 수도 있다. 그런데 약간 문제가 있다.

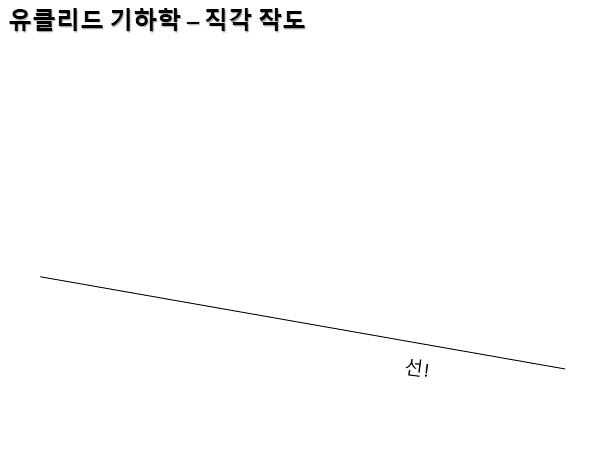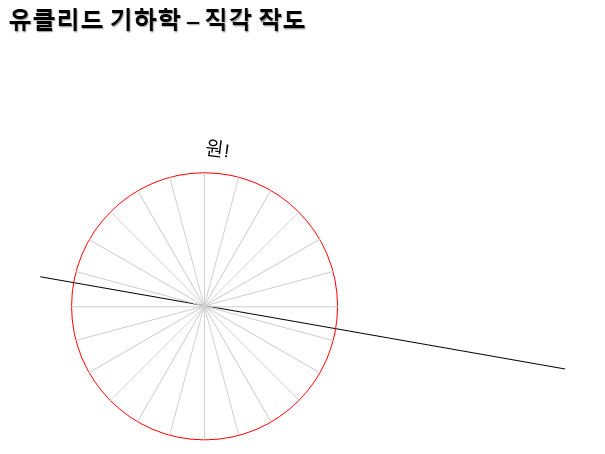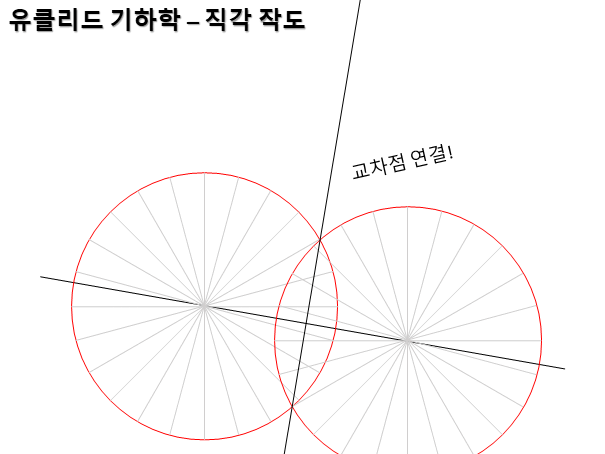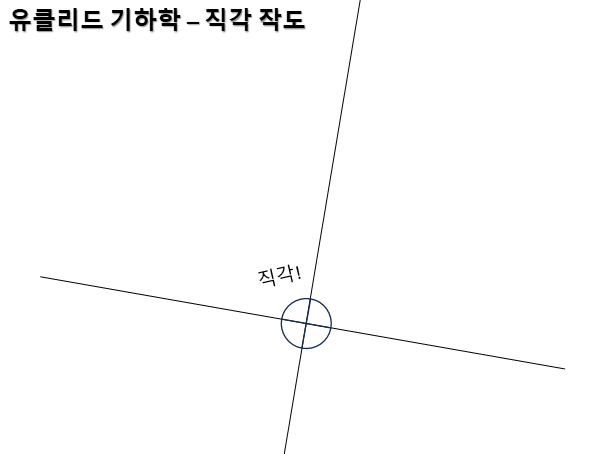
먼저 직각을 그릴 수 있어야 했다. 사각형이 공간 활용 면에서 좋기 때문이다. 석기 시대에는 원을 그리고 집을 지었는데 나중에 사각형 집을 짓는 똑똑한 놈들이 나타나서 밀어낸다. 동서남북을 정확하게 그리기에도 좋으며 기준 축을 삼기에도 좋다.

직각 그리는 방법을 잘 보니 그걸로 선도 2등분할 수 있겠더라. 이렇게 하여서 길이를 정확히 측정할 수 있는 자를 만들 수 있겠다. 2진수이긴 하지만 일단 정확하게 측정을 할 수 있는 자를 만들 수 있으니 좋다. 뭐든 2등분은 쉬운 거 같다. 3등분이 어렵다. 소수(素數)로 나누기는 어렵다. 수에서 원소(元素) 같은 숫자들이다.

각도 2등분 할 수 있게 되어 각도기도 만들 수 있게 되었다. 2진법이긴 하지만 각도를 정확하게 측정할 수 있게 되었다. 수학 삼각함수에서 라디안이 바로 2진법이다. 뭐든 반으로 나누는 것은 쉬운 거 같다. 어떤 꼴통이 각을 3등분할 수 있다고 우기던데 그 친구 주장은 1/2 나누기를 무한 반복해서 1/3에 접근할 수 있다는 것이다. 도달할 수 있는지 죽을 때까지 해 봐라.

같은 원리로 정삼각형도 쉽게 그릴 수 있더라. 이렇게 하여 60도 각도를 그릴 수 있었고, 그 절반인 30도, 그 절반인 15도가 가능해서 각도기에 눈금을 그릴 수 있었다. 90도에 대해서는 3등분이 가능하다. 이리하여 360도를 24등분 할 수 있게 되어 해시계에 하루 시간을 24시간으로 그릴 수 있게 되었고 계절도 24절기로 나누게 된다. 그리고 6각, 12각, 24각 등 2배각을 정확히 그릴 수 있어 원주율도 반복 계산으로 구할 수 있게 되었다.

위의 계산은 원주율 3.141592까지 확정하는데 필요한 반복 회수

3.141까지 확정하는데 6회 반복만 필요함

문제는 (계산기 없이) 제곱근 계산을 해야 하는 피곤함이 있음

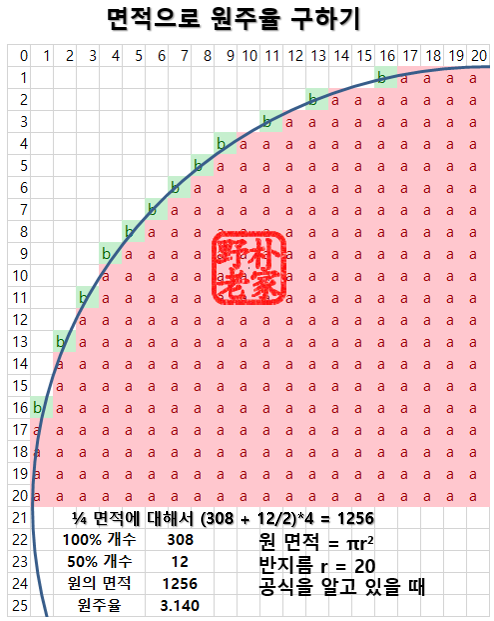
면적으로 원주율을 계산할 수도 있다.

여기서 면적 계산 방법은 첫 번째처럼 삼각형을 반복 계산하는 게 있고,

좀 더 단순 무식하게 원을 가로 세로 격자로 나눈 후에

4각형(1단위 면적)과 3각형(1/2 단위 면적)의 숫자를 세는 방법이 있다.

매우 간단하면서도 정확도가 생각보다 높다는 것.

뉴튼이 발견한 다항식으로 계산하는 방법으로는 매우 많은 계산을 해야 하지만

단순한 가감승제로 계산이 끝난다는 장점이 있음

직각을 2등분하여 대각선을 그릴 수 있어 쉽게 정사각형도 그릴 수 있었다. 이제 원형 집에서 좀 더 공간 활용이 높은 사각형 집에 살 수 있겠다. 특히 정사각형은 면적 계산할 때 매우 편리했다. 작은 정사각형이 몇 개 들어가는지 계산하면 되기 때문이다. 복잡한 모양의 농지(기형적 농지)를 작은 정사각형과 직삼각형으로 나눌 수 있다면 면적 계산이 가능하다. 기형(畸形)이란 단어의 의미가 사각형 면적을 제한 뙈기밭의 형상이란 뜻이다.

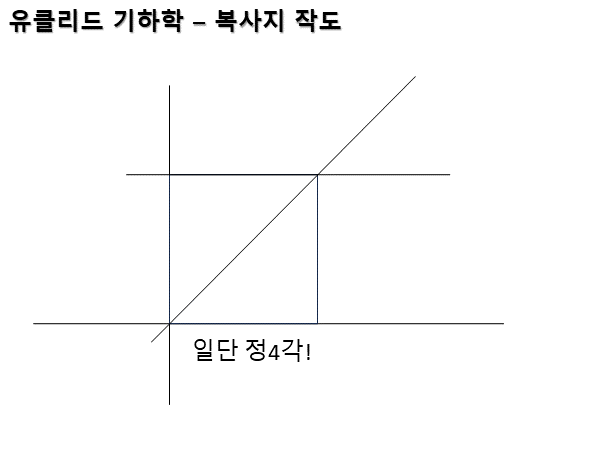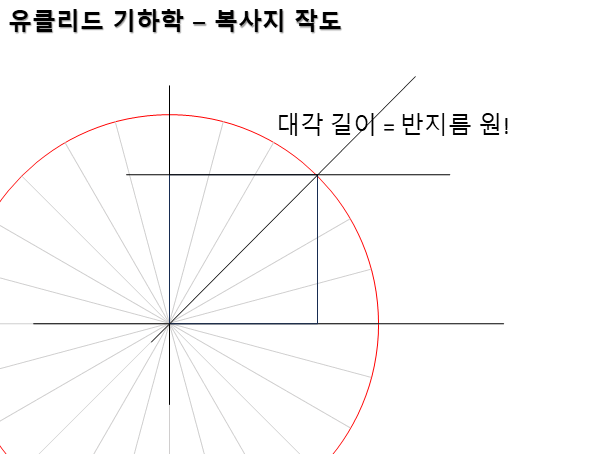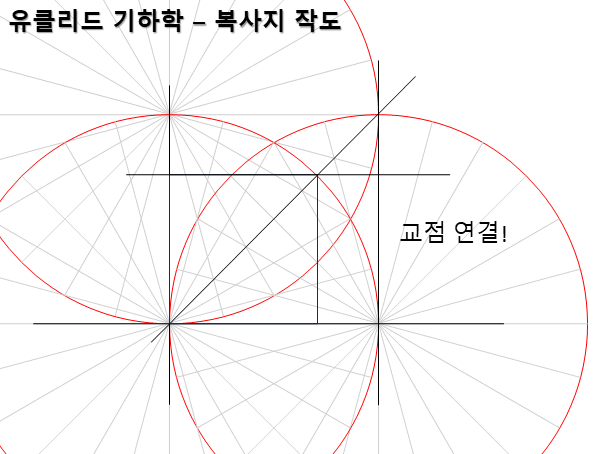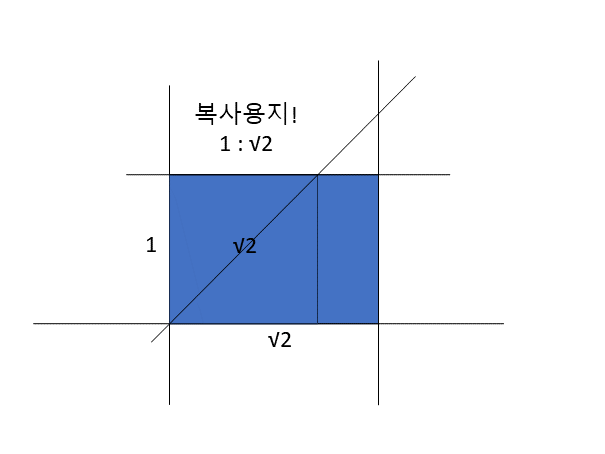
반으로 잘라도 같은 종횡비를 유지하는 것이 복사 용지다. 이건 1과 대각인 √2의 비율이다. 정확히 숫자로 표현하기 무리(無理)하여 무리수(無理數)라 한다. 허나 이 비율의 책상을 2개 붙이면 면적이 2배인 같은 비율의 책상이 된다. 또한 인간의 시야 종횡비인 1.5와 근접한 비율이다. 즉 자연스러운 시야각과 비슷하면서 수학적 의미가 있는 비율이다. 이것도 황금비라 부른다.

전지를 계속 1/2로 자르면 숫자가 커진다

복사지 비율 = √2 = 1.4142135623730950488016887242097

A3 : 297x420mm = A4의 2배

A4 : 210x297mm = A3의 1/2

B4 : 250x353mm = B5의 2배

B5 : 176x250mm = B4의 1/2

B4 ÷ A4 세로 = 1.1904761904761904761904761904762

B4 ÷ A4 가로 = 1.1885521885521885521885521885522

B4 ÷ A4 평균 = 1.1895141895141895141895141895142 = 119%

A4 ÷ B4 평균 = 0.84067933683784876668014557217953 = 84%

보통 들고 다니는 책가방 크기는 애매모호한 B4 크기이다.

B4 용지는 넣을 수 없고, A4 용지를 넣으면 공간이 너무 남는다.

책가방은 책과 비슷한 크기여야 하는 거 아닌가?

사람들이 가장 아름답게 보인다고 주장하는 황금비이다. 특히 정오각형 별이 황금비 덩어리다. 다시 말 해서 황금비를 이용해서 정오각형 별을 그릴 수 있다는 말이다. 정오각형은 실용성은 별로 없다. 신비한 상징으로 많이 사용되어 군대, 공산국가 상징에 많이 보인다. 피타고라스 학파의 상징이었다고 한다. 역시 인간의 시야 종횡비인 1.5와 근접한 비율이다. 즉 자연스러운 시야각과 비슷하면서 정사각형을 빼면 남는 부분이 역시 황금비라는 수학적 의미가 있는 비율이다.

피보나치 수열 = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... (앞의 2개 값을 더한 게 다음 값)

피보나치 수열 = 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... (귀찮아서 처음 0, 1은 생략한다)

황금비 = 피보나치 수열에서 무한 반복한 극한 값 ÷ 바로 앞의 값

황금비 = (√5 + 1)/2 = 1.6180339887498948482045868343656

정5각형과 별 모양에 숨어 있는 황금비를 알아야 정5각형을 그릴 수 있다.

정오각형을 그리려면 원의 반지름과 한 변의 길이의 관계를 알아야 한다. 360도/5=72도 이등변 삼각형의 변들의 길이 비율을 알아야 한다는 말이다. 수학이 발달하지 않았을 시절 이걸 발견할 수 있는 방법은 직접 길이를 측정해서 비교하는 방법이다. 원을 그려 바퀴를 만들어 둘레를 측정하여 원주율 구하는 것과 비슷하다. 그랬더니 황금비의 어느 구석과 일치하는 걸 알았던 거 같다. 증명은 못 하겠지만 같다는 것은 먼저 알 수 있었다. 그러면 작도는 쉽다.

정오각형부터는 그리는 원리를 직관적으로 알기 어렵다. 소수(素數)에 해당하는 각의 도형은 역시 그리기 어렵다. 각도도 2배, 3배, 5배 그리는 것은 쉬운데 역시 나누기가 어렵다. 뭐든 2로 나눌 수 있어 정말 다행이다. 아마 정오각형 작도법을 발견한 후에 신기해서 자신들의 상징으로 사용한 거 같다. 7각형 이상의 작도는 현실에선 쓸모가 없다. 6각형까지 작도가 가능하면 24각형을 작도로 그릴 수 있는데 이게 15도 단위의 시계이며 24절기이다.

원 이외의 곡선 중에 쓸모 있는 게 있는데 타원과 포물선이다. 포물선은 반사 망원경의 거울 만들 때 필요하다. 쌍곡선은 어디에 쓸까? 원을 찌그러뜨리거나 늘리면 타원이 된다. 타원을 아주 길게 만들면 끝 부분은 포물선과 매우 비슷해진다.